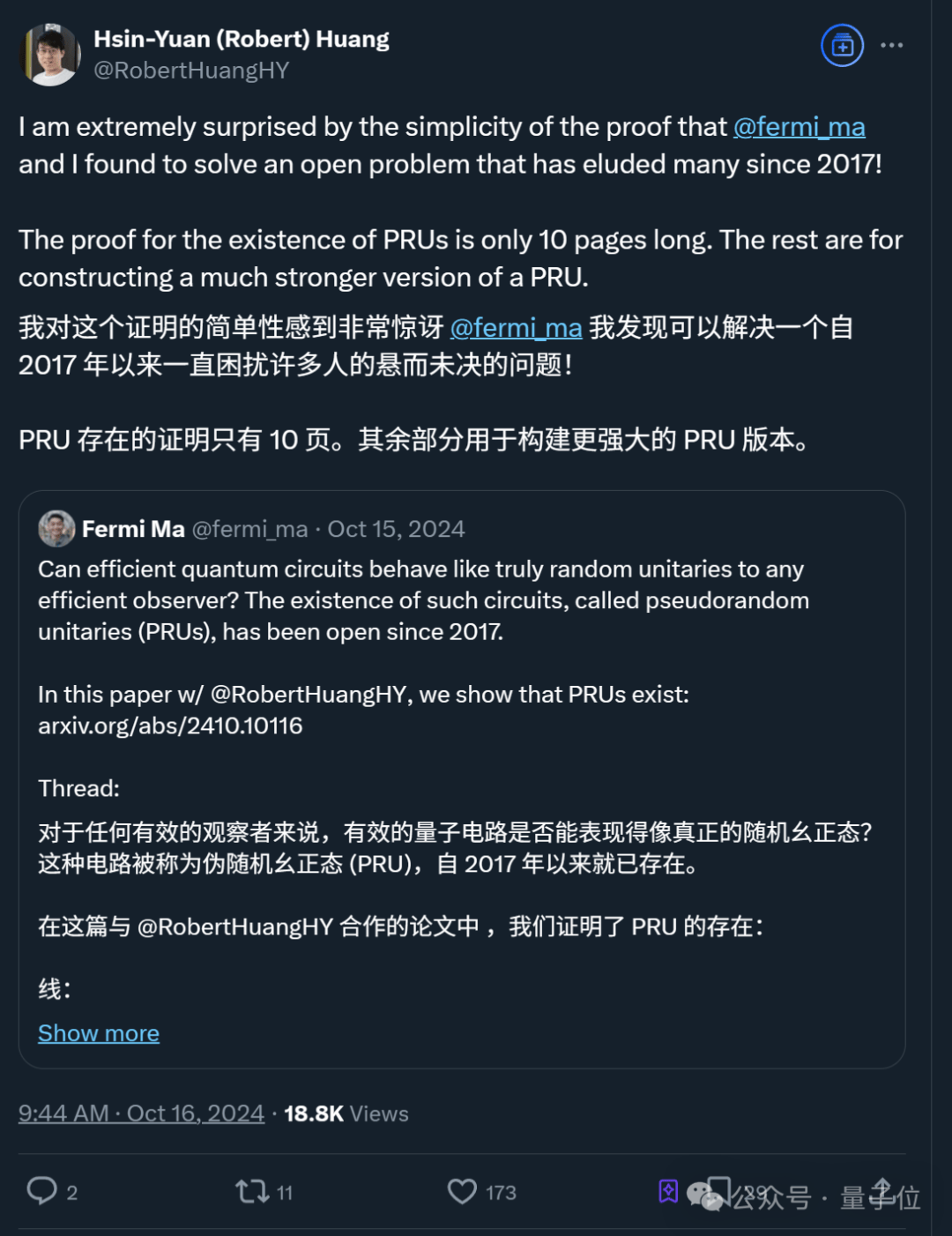
在量子科学领域,一项长期悬而未决的难题似乎已被两位杰出的华人科学家攻克。去年十月,Fermi Ma与黃信元共同发布了一篇革命性的论文,揭示了伪造量子随机性的全新途径。
量子随机性在诸多领域具有不可估量的价值。它不仅能够显著提升算法效率,优化复杂系统模拟,还能验证量子计算的准确性。在密码学领域,量子随机性是生成真正随机密钥的关键,对于保障信息安全至关重要。然而,实现这种随机性的成本高昂,促使科学家们不懈探索伪造随机性的方法。
Ma与黃信元的论文提出了一种前所未有的新方法,据《量子杂志》报道,该方法既优雅又安全,且无需高昂的计算成本。MIT量子计算研究员Alexander Poremba对此赞誉有加,称这是首次有确凿证据证明伪随机性是一个真实存在的概念。

两位科学家在76页的论文中(核心证明仅10页),基于量子安全单向函数的存在假设,成功证明了伪随机幺正态(PRUs)的存在。要理解这一成果,首先需要了解随机幺正的概念。随机幺正在量子计算中至关重要,是量子霸权实验、量子算法和各种加密原语设计的基础。然而,实现随机幺正变换需要巨大的时间和计算资源,因此实际操作极为困难。PRUs的出现为解决这一问题提供了可能。
2017年,一篇论文首次引入了PRUs的概念,并试图通过一种结构上可控的方法来模拟Haar随机酉矩阵。然而,该方法未能完全证明其构造的PRUs与真正的Haar随机酉矩阵等效。在此基础上,Ma与黃信元首次证明了PRUs的存在。
他们的证明过程巧妙运用了量子信息理论中的“净化”技术,并提出了一种名为“路径记录模拟”的新方法。通过记录酉算子在运算过程中的关键信息,他们得以分析酉算子的特点,为后续证明提供了有力支持。借助单向函数这一特殊工具,他们发现了一种之前被认为是“弱伪随机”的构造,实际上具有“真伪随机”的特性,能够在保持简单结构的同时伪装成Haar随机酉矩阵。

两位科学家还证明了一种高效的模拟方法,该方法对于研究Haar随机酉矩阵的量子算法具有极小的模拟误差。这一证明过程涉及对量子算法执行过程的深入研究,以及巧妙利用“路径记录模拟”记录的信息来设计模拟过程。最终,他们通过灵活运用胶合引理,完整地证明了伪随机幺正态的存在。

关于论文的作者,Fermi Ma目前担任西蒙斯-伯克利博士后研究员,于2021年获得普林斯顿大学博士学位,专注于量子计算及其对密码学、复杂性理论和物理学的影响。黃信元则是谷歌量子人工智能的高级研究科学家,这项工作是在他访问西蒙斯计算理论研究所期间完成的。今年,他即将加入加州理工学院担任理论物理学助理教授。